- 토함산 게임
- 토함산 등산로와 마찬가지로 남산 길에서는 포석정에서 시작하는 남산 순환도로가(예전, 박정희 때,, 경주교도소 죄수들을 동원하여 조성한 임도인데) 인위적으로 만들어진 등산로라서 올라가는 재미가 좀 그렇습니다 ㅡㅡ;
- 양자 모두 별 재미는 없는 등산로지만, 석굴암으로 오르는 길의 전체 돌 계단 높이를 일주일 내에 알아오라는 숙제를 주고 불초23 초딩 아덜 중 젤로 또이또이한 세 넘만 뽑아서 빨리 알아오기 시합을 시켜보겠습니다: 매일 새벽 5시에 일어나 새벽을 열어주는 부지런한 재익이, 학교 다닐 때 개근상이란 개근상은 다 도맡아 탄 상구, 오랫동안 조용히 불국사를 지켜온 상문이 이 세 사람이 출발 신호를 기다리고 있는 우리 선수들입니다
- 1. 부지런한 재익이는 새벽 5시에 일어나자 마자 잽싸게 출발합니다: 줄자 하나와 공책 두어 권, 연필 세 자루(및 연필 깎을 칼)을 들고 각각의 돌계단 높이를 줄자로 재어가면서, 또 연필로 공책에 적어가면서(사이사이 연필도 깎을 겸 좀 쉬기도 하면서) 열심히 올라갑니다 - 무려 6일간을 ㅡㅡ; 이제 얼마 안남아서 내일 오전 중으로 끝낼 듯하네요.. 지난 6일간의 지난한 고생들을 생각하니 스스로 대견스럽기도 하고, 또 내일 제일 먼저 답을 제출하여 선생님께 칭찬받을 수 있다는 생각에 뿌듯합니다 - 6일간 올라 다니면서 한번도 상구나 상문이를 못 봤으니, 지넘들이 아무리 열심히 해도 내일 하루만에 이걸 다 잴 수는 없을 터이니 1등은 머 당연지사겠지요?
- 마지막 7일째 날 새벽부터 재익이는 다시 득달같이 달려가 올라가면서 남은 부분들을 재고 있는데.. 정오가 지나자 뒤에서 상구와 상문이가 천천히 걸어 올라옵니다. 속으로 “짜~식들, 인제 와서 언제 다 재겠다고? 내가 1등이야 ㅎㅎ” 코웃음 칩니다. 근데? 저넘들은 계단 높이도 재지 않고 그냥 지나쳐 올라가는 게 아닙니까?? “음~ 포기들 하신 모양이군, 그래 어차피 안되는 거 맘 편히 먹고 등산이나 해서 건강이나 챙겨라” 속으로 위로해주면서 얼마 남지 않은 마지막 고지까지 의기양양 묵묵히 재어갑니다. 휴~ 이제 다 재고 다 적었군요. 진이 다 빠진 채 터벅터벅 밑으로 내려가는데.. 상구하고 상문이는 석굴암 구경까지 하고 놀다 오는지 이제사 저 위에서 내려오고 있군요(“저 게으른 넘들, 안됐따~”)
- 집에 돌아와서는 이불 덮고 엎드린 채로 공책에 적어 놓았던 것들 다 전자계산기로 두드려가면서 보태다 보니 새벽 2시에야 전체 높이 답이 나왔습니다. 자는 둥 마는 둥 잠시 자고, 새벽 5시에 득달같이 일어나 학교에 가서 수업 시작되자마자 의기양양 선생님 앞에 계산 결과를 내밀었는데.. 황당하게도, 상구하고 상문이가 먼저 답을 제출했다는군요. 대체 머야? 저 게으른 넘들은 줄자도 없이 마지막날 하루 오르면서 탱자탱자 놀기만 했는데??
- 선생님한테 들어보니, 상구는 탱자~ 탱자 놀다가 마지막날 오전에 시내로 나가서 고도계를 하나 사서 산에 올랐답니다. 맨 마지막 계단에서 고도계로 고도를 재고, 맨 아래 계단으로 내려와서 또 고도를 재고, 집에 와서 간단히 [맨 위 계단 고도 - 맨 밑 계단 고도 = 전체 계단 높이] 대충 이런 사연이군요(으~ 얍삽한 넘!) - 얍삽한 상구는 다음날 아침에 수업 시작 전 잽싸게 교무실로 방문하여 선생님한테 과제물을 제출했다고 합니다만..
- 상문이는 굳이 고도계 사러 가느라 시간 들이고 버스비 들이고 하는 일도 없이, 조용히 쉬다가 마지막날 정오에 교회에 다녀온 뒤 느긋하게 산에 올랐는데, 계단 맨 위에 올라가서 폰에서 고도 재는 앱 하나 검색해서 깔아서 맨 위와 맨 아래 고도 적고, 그 차이를 폰에 있는 계산기로 풀어 마지막날에 바로 카톡으로 날렸다는군요(으~ 영악한 넘!!)
- 부지런하기만 했던 재익이는 의문의 일패를 당했지만.. 그래도 위로가 되는 건, 위 수수께끼 풀이는 진짜 퀴즈쇼를 위한 힌트였을 뿐이라는 겁니다 - 곧, 위 시합은 진짜 퀴즈쇼를 위한 힌트였기에 모두 무효입니다(대략, 주최측 농간인 듯 ^^). 진짜 시합은 이제부터 시작입니다. 1등한 상문이는 매우 허탈해하고, 2등한 상구는 그냥 시큰둥하게 딴데 보고 있고, 꼴뜽한 재익이는 안도의 한숨을 내쉬고 있군요 ㅎㅎ
- 2. 이제 진짜 상금을 걸고 문제를 내겠습니다: 아래 그림에 있는 9개 분수의 합인 S 값을 구해보십시오 - 아래 식은 9개의 계단 높이를 각각 재서 합하여 전체 높이를 재는 것과 비슷하게 9개 각 분수값의 합을 구하는 문제입니다
- * 힌트를 주자면; 상구 방식이 거기서도, 여기서도 가장 신속하게 또 정확하게 정답을 낼 수 있습니다. 그러면; 계단이 9개가 아니라 9조개일 때라도 1분 이내에 답을 낼 수 있습니다. 미적분의 창시자 라이프니쯔처럼 고민해 보십시오 ㅡㅡ;
- ** 엑셀 쫌 한다면; 재익이 방식의 업그레이드 버전을 쓸 수도 있습니다. 저 9개의 분수들을 하나씩 엑셀에 집어넣고 [자동합계] 내면 간단히 답이 나옵니다 - 물론, 엑셀 ‘쫌’ 하는 수준은 되어야 합니다. 다만, 여기서도 문제는 2번째 분수 \frac{1}{6} 같은 값을 계산하면; 0.1666666667.. 식으로 나온다는 것입니다. 이 값은 수퍼 컴퓨터로 몇 백년 계산해서 소수점 아래 수백 조 이상 자리까지 적어도 결코 끝을 맺을 수는 없다는 단점이 있습니다 - 이른 바, 수학에서 ‘신의 언어’라고 불리우는 (절대 마침표를 찍을 수 없는)‘무리수’입니다 ㅡㅡ;
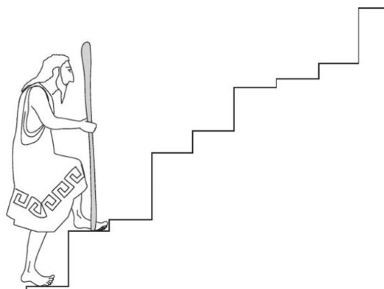
* 일단, 한 노인이 지팡이 짚고 힘겹게 계단을 올라가는 이 그림을 보십시오. 각 계단들의 높이는 다 다릅니다. 이 각각의 계단들 높이를 다 잰 뒤 더해주면 계단 밑에서 맨 위까지의 전체 높이를 알 수 있겠지요? 이 높이 구하기가 오늘의 숙제입니다..
S = \frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + \frac{1}{5 \times 6} + \frac{1}{6 \times 7} + \frac{1}{7 \times 8} + \frac{1}{8 \times 9} + \frac{1}{9 \times 10}
➥ 위 실마리 제시용 장난 수수께끼쇼에서 (부지런한 재익이가 한 것처럼)계단들 높이를 각각 재서 합한 뒤 전체 계단 높이를 낸 것과 같은 방식으로 풀 수도 있고, (얍삽한 상구가 한 것처럼)고도계를 써서 맨 위 고도 값에서 맨 밑 고도 값을 뺄 수도 있습니다 – 머, 적당히 알아서들 계산해보십시오..
 ✓
이 사진 오른쪽편에 보이는 암벽 산이 [상사바위]입니다.
부처님 머리 바로 위 소나무 가지가 보이는 곳은 신선들이 밤에 내려와 바둑을 뒀다는 바둑바위 바로 옆,
옥보고가 밤에 올라 거문고를 뜯었다는 금송정입니다. 이 사진은 부처님 바로 앞에 가서 찍은겁니다.
못 들어가게 줄로 막아 놨지만, 상선암 지나서 한 몇 50여미터 가파른 계단 길 오른 후 휴식 벤치 만들어놓은 평지까지
올라서 ‘들어가지 마시오’라고 줄 쳐진 곳에서 줄 옆으로 살짝 돌아서 한 20여미터만 들어가면 됩니다
- 줄 넘으면 불법이니 줄 옆으로 살~짝 돌아서 들어가셔야 합니다 ^^
✓
이 사진 오른쪽편에 보이는 암벽 산이 [상사바위]입니다.
부처님 머리 바로 위 소나무 가지가 보이는 곳은 신선들이 밤에 내려와 바둑을 뒀다는 바둑바위 바로 옆,
옥보고가 밤에 올라 거문고를 뜯었다는 금송정입니다. 이 사진은 부처님 바로 앞에 가서 찍은겁니다.
못 들어가게 줄로 막아 놨지만, 상선암 지나서 한 몇 50여미터 가파른 계단 길 오른 후 휴식 벤치 만들어놓은 평지까지
올라서 ‘들어가지 마시오’라고 줄 쳐진 곳에서 줄 옆으로 살짝 돌아서 한 20여미터만 들어가면 됩니다
- 줄 넘으면 불법이니 줄 옆으로 살~짝 돌아서 들어가셔야 합니다 ^^


